Il software xFoil è un potentissimo strumento che viene utilizzato in campo aeronautico per la progettazione dei profili alari subsonici. MATLAB è uno dei software più utilizzati nel campo dell’ingegneria. In questo articolo spiegherò come fare ad interfacciare i due software utilizzando la modalità di lavoro batch di xFoil.
Il software xFoil è un potentissimo strumento che viene utilizzato in campo aeronautico per la progettazione dei profili alari subsonici. MATLAB è uno dei software più utilizzati nel campo dell’ingegneria. In questo articolo spiegherò come fare ad interfacciare i due software utilizzando la modalità di lavoro batch di xFoil.
Come appena detto, xFoil dà la possibilità di essere eseguito in modalità batch: un semplice file di testo contenente tutti i comandi in colonna può essere utilizzato come input del programma, che eseguirà il tutto in sequenza.
Il collegamento con MATLAB consiste nel creare il file di testo contenente i comandi, esportare i risultati di xFoil in dei file di testo e infine importare questi file all’interno di MATLAB.
I comandi principali che utilizzeremo per fare ciò sono:
- fopen e fprintf per creare un file di testo
- !xfoil < batch.dat per eseguire xFoil
- importdata per importare i risultati
L’esempio pratico che andremo a considerare prevede l’importazione del coefficiente di pressione su un profilo NACA 4412 calcolato tra alfa=-10° e alfa=15°, in modalità viscosa con numero di Reynolds pari a 10^6.
Il codice
Scaricabile da questo link: Download script MATLAB-xfoil.zip
Mostra codice ▼
% Generazione e importazione di dati con il software xFoil
% Script elaborato da Alessandro Masullo, 03/12/2012
% Web: https://www.wirgilio.it
%
% Questo script crea un file di comandi per xFoil, lo esegue e importa i
% risultati nel workspace.
% Una cartella "dati" viene creata per includere i risultati di xFoil
% Un file di testo "comandi.dat" contiene i comandi che vengono fatti
% eseguire ad xFoil. In particolare viene esportato il diagramma del
% coefficiente di pressione di un NACA 4412 tra alfa -10 e alfa 15 con
% passo 0.5 a Reynolds 10^6
clc; clear;
%% Scrittura dei dati
% Crea una cartella per contenere i risultati di xFoil
if not(isdir('./dati')), mkdir('./dati'); end
% Comandi di xFoil
alfa = -10:0.5:15;
N = length(alfa);
comandi = {
'NACA 4412'
'OPER'
'RE 1e6'
'VISC ON'
sprintf(['ALFA %.3f\n' ...
'CPWR ./dati/cp(%d).dat\n'], [alfa; 1:N])
'QUIT'
};
% Scrive i comandi nel file
id = fopen('comandi.dat', 'w+');
fprintf(id, '%s\n', comandi{:});
fclose(id);
% Esegue xfoil
!xfoil.exe < comandi.dat
%% Legge i risultati
% Apre in sequenza tutti i file generati da xfoil e li mette in un cell
% array
dati = cell(1, N);
for i = 1:N
% La variabile foo è di appoggio e serve a importare il solo contenuto
% numerico dei file generati da xfoil
foo = importdata(sprintf('./dati/cp(%d).dat', i), ' ', 1);
dati{i} = foo.data(:, : );
end
%% Post-processing
figure(1)
for i = 1:N
plot(dati{i}(:, 1), dati{i}(:, 2), '-k')
% Asse negativo verso il basso
set(gca, 'ydir', 'reverse')
% Calcola il cl da mettere nel titolo
cl = trapz(dati{i}(:, 1), dati{i}(:, 2));
title(sprintf('Diagramma del cp a cl = %.3f', cl))
axis([0 1 -5 1])
pause(0.5)
end
La spiegazione del codice
Per prima cosa, creiamo una variabile (cell array) contenente tutti i comandi da eseguire all’interno di xFoil. La variabile comandi è molto intuitiva e potrebbe essere utilizzata inserendo tutti i singoli comandi uno ad uno, ma la comodità di utilizzare MATLAB sta proprio nel non dover inserire manualmente i comandi ripetitivi, come ad esempio una sequenza di:
alfa 0
cpwr alfa(0).dat
alfa 0.1
cpwr alfa(1).dat
... e così via
Per cui, inseriamo manualmente i comandi principali, come la scelta del profilo e i parametri di viscosità, e utilizziamo la funzione sprintf per scrivere una sequenza di angoli di attacco.
comandi = {
'NACA 4412'
'OPER'
'RE 1e6'
'VISC ON'
};
La funzione sprintf, originaria del C, crea una stringa a partire da un modello contenente delle variabili. La sintassi è:
sprintf('stringa modello', var1, var2, ..., varN')
La struttura della stringa modello contiene una serie di “segnaposto”, identificati dal simbolo % (percento), all’interno del quale vengono inserite le variabili passate alla funzione come argomento. Es.:
sprintf('Il mio nome è %s, ho %d anni e sono alto %.2f m', 'Ale', 8, 1.753)
Il mio nome è Ale, ho 8 anni e sono alto 1.75 m
Il segnaposto %s sta per stringa, %d sta per numero intero, %.2f sta per numero decimale con 2 cifre dopo la virgola.
Nel nostro caso la stringa che vogliamo generare è:
alfa -10
cpwr cp(1).dat
alfa -9.5
cpwr cp(2).dat
...
Abbiamo quindi bisogno di un vettore contenente gli angoli di attacco (da -10 a 15 con passo 0.5)
alfa = -10:0.5:15
E un vettore di indice (da 1… a quanti sono gli alfa)
N = length(alfa)
indice = 1:N
Per praticità, utilizzeremo una caratteristica del modo di funzionare di sprintf su MATLAB. Se sprintf riceve come argomento una matrice, i valori che metterà nei segnaposto saranno gli elementi della matrice, presi in ordine procedendo lungo le colonne.
Dato che la nostra stringa vede in sequenza l’angolo d’attacco e il suo indice, potremo utilizzare una matrice di questo tipo:
[alfa(1), alfa(2), ..., alfa(n);
1, 2, ..., n]
Sarà interpretato come:
alfa(1), 1, alfa(2), 2, ... alfa(n), n
Per generare la sequenza di angoli d’attacco sarà quindi sufficiente utilizzare il comando:
sprintf('ALFA %.3f\nCPWR ./dati/cp(%d).dat\n', [alfa; 1:N])
Dove il simbolo \n sta per “a capo”.
Da cui l’espressione completa dei comandi:
alfa = -10:0.5:15;
N = length(alfa);
comandi = {
'NACA 4412'
'OPER'
'RE 1e6'
'VISC ON'
sprintf(['ALFA %.3f\n' ...
'CPWR ./dati/cp(%d).dat\n'], [alfa; 1:N])
'QUIT'
};
Questi comandi vanno inseriti in un file di testo, per cui creiamo un nuovo file e inseriamovi il contenuto della variabile comandi:
id = fopen('comandi.dat', 'w+');
fprintf(id, '%s\n', comandi{:});
fclose(id);
Infine, eseguiamo xFoil con questo comando:
!xfoil.exe < comandi.dat
Attenzione! Affiché questo comando venga eseguito correttamente, il file eseguibile xfoil.exe deve essere collocato nella vostra cartella di lavoro. Per conoscere la vostra cartella di lavoro digitate pwd nella command window.
Se è andato tutto a buon fine, nella cartella di lavoro dovreste trovarvi una nuova cartella, dati, contenente un bel po’ di file cp(x).dat. Sono ovviamente i file generati da xFoil.
A questo punto non ci resta che importare i risultati. Per fare ciò utilizzeremo la funzione importdata, la cui sintassi è:
importdata('nome del file', 'delimitatore', righe di intestazione)
Nel nostro caso il nome del file è una stringa del tipo cp(%d).dat, dove %d è un numero che va da 1 a quanti sono gli alfa.
Per importare tutti i file sarà sufficiente un ciclo for che, da 1 ad N, importa tutti i risultati di xFoil e li carica in un cell array di nome dati:
dati = cell(1, N);
for i = 1:N
% La variabile foo è di appoggio e serve a importare il solo contenuto
% numerico dei file generati da xfoil
foo = importdata(sprintf('./dati/cp(%d).dat', i), ' ', 1);
dati{i} = foo.data(:, : );
end
Come esplicitato nel commento, importdata cercherà di importare anche la prima riga di testo di ogni file, la quale ci ricorda che la prima colonna contiene le ascisse e la seconda i valori del Cp. Per evitare di importare tra i dati anche questa stringa di testo inseriamo il solo valore data all’interno dell’array di dati.
L’ultima parte del codice si limita a fare una serie di diagrammi in sequenza dei vari Cp calcolati da xFoil.
È possibile scaricare un archivio contenente questo script funzionante e la versione eseguibile di xFoil per Windows al seguente link:
Download script MATLAB-xfoil.zip
Variazione del numero di Reynolds
Ho ricevuto un’e-mail in cui mi si chiedeva una modifica del codice che permettesse la variazione del numero di Reynolds. Ho pensato che potesse essere utile anche a qualcun altro, e così l’ho pubblicata qui.
Non sarà certo il modo più elegante di farlo, ma le modifiche al codice sono minimizzate! La matrice matp, che viene letta da fprintf lungo le colonne, ha questa struttura:
Re(1) Re(1) Re(1)
alfa(1) alfa(2) alfa(3)
1 4 7
Re(2) Re(2) Re(2)
alfa(1) alfa(2) alfa(3)
2 5 8
Re(3) Re(3) Re(3)
alfa(1) alfa(2) alfa(3)
3 6 9
Mostra codice ▼
clc; clear;
%% Scrittura dei dati
% Crea una cartella per contenere i risultati di xFoil
if not(isdir('./dati')), mkdir('./dati'); end
% Comandi di xFoil
alfa = 0:15;
Re = [1e5 5e5 1e6 5e6 1e7 5e7 1e8 1e9];
Na = length(alfa);
NRe = length(Re);
N = NRe*Na;
matp = zeros(NRe*3, Na);
matp(1:3:end-2, : ) = repmat(Re', 1, Na);
matp(2:3:end-1, : ) = repmat(alfa, NRe, 1);
matp(3:3:end, : ) = reshape(1:N, NRe, Na);
comandi = {
'NACA 4412'
'OPER'
'ITER 200'
'VISC'
'1e6'
sprintf(['RE %g\n' ...
'ALFA %.3f\n' ...
'CPWR ./dati/cp(%d).dat\n' ...
'INIT\n'], matp)
'QUIT'
};
% Scrive i comandi nel file
id = fopen('comandi.dat', 'w+');
fprintf(id, '%s\n', comandi{:});
fclose(id);
% Esegue xfoil
!xfoil < comandi.dat
%% Legge i risultati
% Apre in sequenza tutti i file generati da xfoil e li mette in un cell
% array
dati = cell(1, N);
for i = 1:N
% La variabile matp è di appoggio e serve a importare il solo contenuto
% numerico dei file generati da xfoil
foo = importdata(sprintf('./dati/cp(%d).dat', i), ' ', 1);
dati{i} = foo.data(:, : );
end
%% Post-processing
figure(1)
for i = 1:N
plot(dati{i}(:, 1), dati{i}(:, 2), '-k')
% Asse negativo verso il basso
set(gca, 'ydir', 'reverse')
title(sprintf('Diagramma del cp ad alfa = %.1f, Re = %g,', matp(3*i-1), matp(3*i-2)))
axis([0 1 -5 1])
pause(0.5)
end
Suggerimenti
Ai fini delle prestazioni, xFoil risulta estremamente più veloce se sopprimete l’output grafico, che vi sarà probabilmente inutile se avete intenzione di lavorare con MATLAB sui risultati.
Per fare ciò, potete inserire questi tre elementi ai primi comandi della variabile comandi:
comandi = {
'plop'
'g'
''
% tutto il resto
}
Accertatevi inoltre, specialmente se disabilitate l’output grafico, che nei casi estremi che andate a studiare xFoil giunga a convergenza, altrimenti importerete dei risultati che potrebbero essere sballati!
Scegliete quindi un numero di iterazioni opportunamente elevato per assicurarvi di ciò.

 Entrambi i motori funzionano sfruttando il Terzo Principio della Dinamica: se salgo sui pattini e lancio un grosso masso in avanti, per il principio di azione e reazione riceverò una spinta all’indietro che mi farà muovere nella direzione opposta alla pietra. Se invece di lanciare pietre aziono un estintore, l’effetto è lo stesso: il gas va da una parte, io vengo spinto dall’altra. La stessa cosa succede con i motori di razzi e aerei.
Entrambi i motori funzionano sfruttando il Terzo Principio della Dinamica: se salgo sui pattini e lancio un grosso masso in avanti, per il principio di azione e reazione riceverò una spinta all’indietro che mi farà muovere nella direzione opposta alla pietra. Se invece di lanciare pietre aziono un estintore, l’effetto è lo stesso: il gas va da una parte, io vengo spinto dall’altra. La stessa cosa succede con i motori di razzi e aerei.


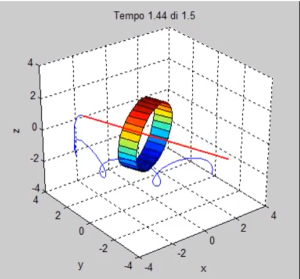
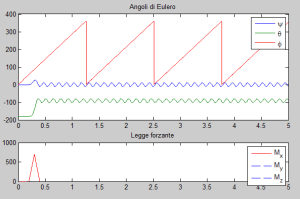 Prima di procedere con l’animazione è necessario conoscere un comportamento peculiare di ode45: insieme al vettore Y contenente le variabili di stato integrate, viene restituito anche un vettore temporale T cui corrispondono gli istanti di tempo relativi ad Y. Questo vettore è, generalmente, non lineare. ode45 ha infatti la capacità di modificare il passo di integrazione rendendolo più o meno fitto a seconda della variazione del vettore di stato. Se utilizzassimo questo vettore senza modificarlo, il risultato sarebbe un video che va piano quando ci sono variazioni irregolari di Y e veloce quando Y è più regolare.
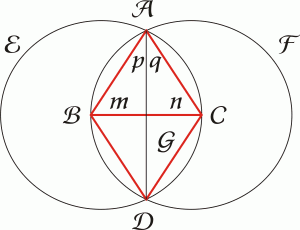
Prima di procedere con l’animazione è necessario conoscere un comportamento peculiare di ode45: insieme al vettore Y contenente le variabili di stato integrate, viene restituito anche un vettore temporale T cui corrispondono gli istanti di tempo relativi ad Y. Questo vettore è, generalmente, non lineare. ode45 ha infatti la capacità di modificare il passo di integrazione rendendolo più o meno fitto a seconda della variazione del vettore di stato. Se utilizzassimo questo vettore senza modificarlo, il risultato sarebbe un video che va piano quando ci sono variazioni irregolari di Y e veloce quando Y è più regolare. Spesso i giroscopi si studiano utilizzando un sistema di riferimento diverso da quello utilizzato da me. Si considera il giroscopio montato su uno snodo cardanico (vedi figura) e si scrivono angoli e momenti rispetto agli assi degli snodi.
Spesso i giroscopi si studiano utilizzando un sistema di riferimento diverso da quello utilizzato da me. Si considera il giroscopio montato su uno snodo cardanico (vedi figura) e si scrivono angoli e momenti rispetto agli assi degli snodi.