Siamo a Copenhagen, facoltà di Fisica, durante la prova scritta di un esame.

Traccia del problema
“Descrivere come determinare l’altezza di un grattacielo con un barometro.”

Risposta di uno studente
“Si lega un lungo pezzo di spago al collo del barometro, poi si cala il barometro dal tetto del grattacielo fino al suolo. La lunghezza dello spago più la lunghezza del barometro saranno uguali all’altezza del palazzo”

Lo studente viene bocciato ma fa ricorso. La Commissione esamina il ricorso e stabilisce che la risposta è corretta, ma non mostra una conoscenza esplicita della fisica. Lo studente ha perciò diritto ad una prova d’appello:
“Per dimostrare familiarità con i principi fondamentali della fisica lo studente risponda alla stessa domanda in un tempo massimo di 6 minuti”

Lo studente rimane in silenzio per 5 minuti, scrive qua e là su un foglio di carta e poi, prima dello scadere del tempo risponde:
«Ci sono molti modi di rispondere alla domanda, e non riesco a scegliere quale. Comunque, si potrebbe portare il barometro sul tetto del grattacielo, lasciarlo cadere giù e misurare il tempo che impiega a raggiungere il suolo. L’altezza del grattacielo può essere determinata dalla formula che ho elaborato su questo foglio. Tuttavia, non sarebbe salutare per il barometro.

Una soluzione alternativa è questa: se c’è il sole si potrebbe misurare l’altezza del barometro e la lunghezza della sua ombra quando è in piedi. Poi si misura la lunghezza dell’ombra del grattacielo e con una semplice proporzione geometrica si ottiene l’altezza del grattacielo. La formula per calcolarla è sul foglio, sotto alla precedente.

Tuttavia, se proprio vogliamo essere molto scientifici, si potrebbe legare un pezzo di spago al barometro e farlo oscillare come un pendolo, prima al piano terra e poi sul tetto.
L’altezza del grattacielo potrebbe poi essere determinata dalla differenza nella formula gravitazionale che ho derivato su quest’altro foglio di carta. Mi scuso per il calcolo lungo e complesso.

Però c’è anche un altro modo non disprezzabile. Se il grattacielo ha una scala di emergenza, sarebbe più semplice salire le scale e misurare l’altezza del palazzo utilizzando l’altezza del barometro come unità di misura.

Ma se davvero si vuole essere noiosi e ortodossi, si potrebbe sempre utilizzare il barometro per misurare la pressione atmosferica sul tetto, poi al suolo e convertire la differenza di millibar in metri, così da ottenere l’altezza del palazzo.

Tuttavia, dal momento che il nostro insegnante ci esorta continuamente ad essere creativi nell’applicazione dei metodi scientifici, il modo indubbiamente migliore sarebbe quello di bussare alla porta del custode del palazzo e chiedergli: “Le interesserebbe un nuovo barometro? Posso regalarle questo, se mi dice l’altezza del palazzo…“»

La Commissione delibera che lo studente debba essere promosso col massimo dei voti.
Lo studente era Niels Henrik David Bohr, Premio Nobel per la fisica nel 1922 per i suoi studi sulla struttura atomica e sull’atomo di idrogeno.

Ho già parlato delle potenzialità di Wolfram Alpha in un precedente articolo, ciò che voglio fare ora è descriverne il suo funzionamento finalizzato all’esame più temuto al primo anno delle facoltà scientifiche: Analisi matematica.

Innanzitutto, è importante sapere che tutte le operazioni matematiche svolte da Wolfram Alpha, sono eseguite da Wolfram Mathematica, un software commerciale della Wolfram. La sintassi di Wolfram Alpha non è la stessa di Mathematica, ma essendo in grado di comprendere quasi ogni tipo di richiesta, spesso riesce ad interpretare anche la sintassi di Mathematica.

I comandi che utilizzo in questo articolo come input per Wolfram Alpha non sono gli unici comandi che si possono utilizzare per ottenere lo stesso risultato. Ad esempio, se voglio calcolare la somma di due numeri, posso scrivere “4+9“, “sum of 4 and 9“, “what is the sum of 4 and 9?” o ancora “can you tell me the sum of 4 and 9?“.
Se trovate dei comandi più intuitivi di queli che ho utilizzato io, ben venga :).

Funzioni

La prima cosa che possiamo provare a fare con Wolfram Alpha è uno studio di funzione.
Consideriamo la funzione:

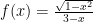
Inserendo l’espressione di questa funzione in Wolfram Alpha (link), il programma ci fornirà una serie di informazioni utili per lo studio della funzione:

• Input: è la funzione che abbiamo appena inserito.
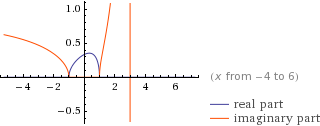
• Plots: una serie di grafici caratteristici della funzione. Il primo per x da -4 a 6, il secondo per x da -40 a 40. Gli estremi dei grafici variano a seconda della funzione e sono generati in modo da permettere una visione di tutte le sue particolarità.
  Entrambi i grafici sono costituiti da una linea rossa e una linea blu. Se si considera la funzione definita solo in un sottoinsieme dei numeri reali, il dominio è a causa della radice, e il grafico è rappresentato dalla linea blu. Se però consideriamo la funzione in un sottoinsieme dei numeri complessi, la radice è definita sempre e l’unica limitazione del dominio è 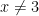. La linea rossa rappresenta quindi la parte immaginaria della funzione e in è tracciata una linea verticale che ne costituisce un asintoto.
  
• Alternate forms: una serie di espressioni alternative con le quali possiamo esprimere la nostra funzione. È molto utile ad esempio se la nostra funzione va considerata in un prodotto di funzioni e ci sono elementi che si possono semplificare.
• Roots: sono le radici (o zeri) della funzione, ossia i valori delle x per i quali la funzione vale zero.
• Series expansion at x = : è lo sviluppo in serie di Taylor della funzione, con punto di partenza in alcuni valori caratteristici della funzione come le radici, l’origine e all’infinito.
  Per calcolare lo sviluppo in serie di Taylor con un punto di partenza diverso, basta scrivere “f(x) series expansion in x=k“, dove f(x) è la nostra funzione e k il punto di partenza che ci interessa (link).
  Verrà inoltre effettuato un grafico di confronto tra la funzione e i suoi sviluppi in serie di primo e secondo ordine:
  
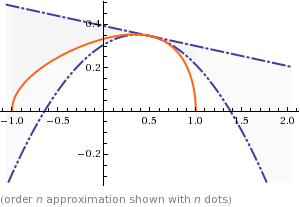
• Derivative: è la derivata della funzione rispetto ad x.
• Indefinite integral: è l’integrale indefinito della funzione, ossia una sua primitiva. Notare che e sono rispettivamente Arcotangente e Arcoseno, come è scritto in basso a destra.

Conoscere l’espressione della derivata e dell’integrale di una funzione è senza dubbio un’informazione notevole, per chi è alle prese con uno studio di funzione. Ma un’informazione ancora migliore sarebbe conoscere i passaggi da seguire per arrivare all’espressione di quella derivata o integrale. Ebbene, Wolfram Alpha ci fornisce persino questa informazione.
Cliccando infatti su Show steps verranno mostrati tutti i passaggi che bisogna seguire per risolvere quella derivata o quell’integrale.
Per l’integrale suggerisce infatti di effettuare prima una sostituzione trigonometrica, poi una seconda sostituzione e infine mostra il valore di ogni integrale che permette di arrivare alla soluzione finale (link).
(beh, sì, ho inventato una funzione che ha un integrale davvero particolarmente complesso!)

• Global maximum/minimum: sono i punti di massimo e minimo assoluti della funzione, con i rispettivi valori.
• Limit: sono dei limiti della funzione calcolati a e 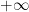. Ovviamente viene considerata la parte immaginaria della funzione, dato che la parte reale è definita soltanto tra -1 e +1.
• Series representations: un’altra rappresentazione in serie della funzione.
• Property: nel caso in cui la funzione soddisfi particolari proprietà di simmetria o periodicità, queste verranno indicate sotto questa voce. Ad esempio, nel caso del seno, ci informa che questo è periodico di (link).

Integrali e derivate

Abbiamo già visto come nello studio di funzione Wolfram Alpha sia in grado di calcolare, tra le varie cose, un integrale o una derivata.
Se però abbiamo bisogno di maggiori informazioni su un integrale o una derivata, basterà inserire come input “integrate f(x)“, oppure “derivate f(x)“, dove f(x) è la nostra funzione (link 1, link 2).

Come prima, dopo aver calcolato il valore della derivata o dell’integrale con tanto di passaggi intermedi, verranno riproposte una serie di informazioni relative allo studio di funzione, dove questa volta la funzione studiata è la derivata o l’integrale della funzione che stavamo studiando. E quindi: grafico, forme alternative, radici, sviluppi in serie, ecc…

Potrebbe essere necessario però calcolare il valore di un integrale definito.

Basterà inserire come input “integrate f(x) from a to b“, dove a e b sono i nostri estremi di integrazione (link).
Verrà mostrato il valore numerico dell’integrale e una sua rappresentazione grafica.
Qualora il risultato dovesse essere espresso in forma decimale, è possibile mostrare quante cifre decimali si desidera cliccando su More digits.

Un’altra operazione interessante è quella di derivata parziale. Se abbiamo infatti una funzione definita in :

Per avere la derivata rispetto ad x, basta scrivere “derivate f(x,y) in x” e quella rispetto ad y “derivate f(x,y) in y” (link).

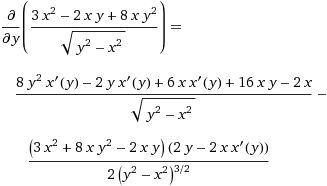
Ancora una volta, con i relativi passaggi (Show steps).

Risoluzione di equazioni

Wolfram Alpha offre una quantità inimmaginabile di strumenti matematici. Uno dei più semplici e più utilizzati, è la risoluzione di equazioni.
Risolvere un’equazione è semplicissimo, basta digitare “solve eq(x)“, dove eq(x) è la nostra equazione (link).
Oltre alle soluzioni reali, verranno ovviamente fornite anche le soluzioni in campo complesso.

Per risolvere un sistema di equazioni, siano esse di qualsiasi tipo, basta scrivere le equazioni separate da una virgola.
Esempio: “solve x+3y=5, 4x-8y=0” (link).

Oltre alla risoluzione di equazioni tradizionali, Wolfram Alpha è in grado di risolvere molti altri tipi di equazioni, come ad esempio le equazioni differenziali. Per risolvere, ad esempio, questa equazione differenziale:

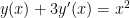
basta digitare “solve y(x)+3y'(x)=x^2” (link). Verrà restituito il tipo di equazione differenziale (nel nostro caso ordinaria lineare di primo ordine), l’insieme di funzioni che soddisfano l’equazione (se esiste), il grafico di una delle soluzioni con la relativa derivata, e un grafico dell’andamento di queste funzioni:

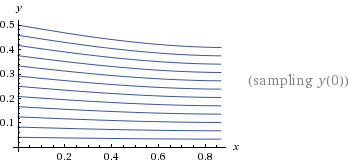
Le capacità di Wolfram Alpha non si fermano neanche davanti ad un’equazione differenziale non lineare di terzo ordine, come l’Equazione di Blasius:

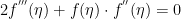
Questa equzione non ha soluzioni analitiche, ma esclusivamente numeriche.
Wolfram Alpha non dà la soluzione numerica (forse sarebbe troppo!) ma ci fornisce comunque un grafico dell’andamento della funzione e delle sue derivate (link).

Per informazione, l’equazione può essere risolta comunque semplicemente utilizzando Wolfram Mathematica, con i tre seguenti comandi:

sol=NDSolve[{f'''[x]+0.5f[x]*f''[x]==0,f'[0]==0,f[0]==0,f'[50]==1},f,{x,0,10}]
b[x]=f[x]/.sol
Style[TableForm[{Table[x,{x,0.1,8,0.2}],Table[{Evaluate[f[x]/.sol]},{x,0.1,8,0.2}],Table[{Evaluate[f'[x]/.sol]},{x,0.1,8,0.2}],Table[{Evaluate[f''[x]/.sol]},{x,0.1,8,0.2}]},TableDirections->Row,TableHeadings->{{"n", "f", "f'", "f''"},None}],12]

Successioni e serie numeriche

Per quanto riguarda successioni e serie numeriche, l’informazione che generalmente interessa lo studente di Analisi è la convergenza.

– Per le successioni, basta calcolare un limite. Il comando per risolvere un limite è “limit f(n) n to k“, dove f(n) è la successione, k è il valore a cui fate tendere n (per infinito, è infinity).
Ad esempio, per la successione:

basta digitare “limit n/(n+1) n to infinity” (link).

– Per le serie numeriche il comando è “sum f(n) n to infinity“. Ad esempio per:

basta digitare “sum 1/(n^2+1)” (link).
Anche qui, come per integrali e derivate, le informazioni fornite sono molto interessanti:

• Infinite/approximate sum: il valore della sommatoria in forma analitica (se esiste) e decimale.
• Finite sum approximation: è una stima della somma per valori di n finiti. (il suo valore non indica che la serie converge!)
• Convergence tests: questa voce è molto interessante, perché ci informa di quali criteri di convergenza sono stati applicati, e quali di questi sono soddisfatti.
• Partial sums: è un grafico delle somme parziali che mette in mostra l’andamento della serie.
• Partial sum formula: è un’espressione per le somme parziali.

Infine, ecco il link del portentoso strumento:
http://www.wolframalpha.com

In qualche ora di tempo libero ho scritto questo semplice giochino in Python. Dovrebbe rappresentare il gioco del Sette e mezzo ma, anche se le modalità di gioco sono quelle, non sono sicuro che a livello probabilistico sia lo stesso.

Il gioco si svolge contro il computer: prima vengono distribuite le due carte, poi il giocatore può richiederne altre finché non è soddisfatto del suo punteggio.
Successivamente il banco richiede le sue carte finché non si rivelano i punteggi.

Le carte fino a 7 corrispondono a un punteggio del loro valore, le carte 8, 9 e 10 corrispondono a mezzo punto.
Vince il giocatore con il punteggio maggiore, ma se si supera il punteggio di 7 e mezzo si perde, e in caso di punteggio pari vince il banco.

from random import randint
deck = [4 for foo in range(10)]
score = 0.0
dscore = 0.0

def give_card():
    # Return a card and remove it from the deck
    global deck
    while any(deck):
        card = randint(0, 9)
        if deck[card] > 0:
            deck[card] -= 1
            return card

def cscore(hit, score):
    # Calculate the score
    if hit < 7:
        return score + hit + 1
    else:
        # Gold King
        if hit == 10 and randint(0, deck[9]-1) == 0:
            print 'E\' uscita la matta!'
            return 7
        else:
            return score + 0.5

while True:
    print '***************************************'
    # I need first card value because dealer can't see it
    your_card = fcard = give_card()
    score = cscore(your_card, score)
    dealer_card = give_card()
    dscore = cscore(dealer_card, dscore)
    print 'Tua carta: %d (%.1f)' % (your_card+1, score)
    # Card request
    while True:
        # Your turn
        if raw_input('\nAltra carta? [y/n] ') == 'y':
            your_card = give_card()
            print '[Carta] %d' % (your_card+1)
            score = cscore(your_card, score)
            print 'Punteggio: %.1f' % score
            if score > 7.5:
                print '**** Hai sballato! ****'
                break
        # Dealer turn
        else:
            # Dealer ask for a card if his score is lower then your shown score
            # Dealer may think you are bluffing (randint)
            print 'Il banco ha: %d (%.1f)' % (dealer_card+1, dscore)
            while dscore < score - cscore(fcard, 0) or randint(0, 3) == 0\
                  and dscore < 7.5:
                dealer_card = give_card()
                print '[Carta] %d' % (dealer_card+1)
                dscore = cscore(dealer_card, dscore)
                if dscore > 7.5:
                    break
            print 'Punteggio del banco: %.1f' % dscore
            if score > dscore or dscore > 7.5:
                print '\o/ \o/ \o/ Hai vinto! \o/ \o/ \o/'
            else:
                print '**** Hai perso! ****'
            break
    # Game request
    if raw_input('\nGiochi ancora? [y/n] ') == 'y':
        score = 0.0
        dscore = 0.0
        print '\n'
    else:
        break

“Qualcuno volò sul nido del cuculo” di Milos Forman, probabilmente il più grande film riguardante la materia. Con un Jack Nicholson da brividi;

“L’esercito delle 12 scimmie” di Terry Gilliam, la prima parte è uno schizzo della malattia mentale in generale, con un ottimo Brad Pitt, ma comunque inferiore rispetto a “Fight Club”;

“A beautiful mind” di Ron Howard, chi lo ha detto che lo schizofrenico è pazzo?;

“Ragazze interrotte” di James Mangold, aiuta a capire perchè il “disturbo di personalità borderline” è anche chiamato “disturbo spazzatura”;

“Will Hunting – Genio ribelle” di Gus Van Sant, non sono un grande fan di Robin Williams, ma l’oscar per miglior attore non protagonista qui se lo meritò, guarda caso il suo unico oscar;

“The Jacket” di John Maybury, i farmaci non sempre migliorano le cose, anzi…;

“K-PAX” di Ian Softley, i film con Kevin Spacey andrebbero visti a prescindere ( a riguardo consiglio due “off-topic”, “I Soliti Sospetti” e “American Beauty” ), poi se c’è di mezzo anche l’ipnosi, diventa un “must-see”;

“Il quarto tipo” di Olatunde Osunsanmi, utile per capire la potenza dell’ipnosi, anche se poi le testimonianze si sono rivelate false;

Infine due film “mezzi off-topic”:

“Quills” di Philip Kaufman, il marchese De Sade è un uomo il cui peso storico è stato ampiamente sottovalutato: SVEGLIA… il sadismo è insito nella natura umana!

“Apocalypse Now” ( versione originale ) di Francis Ford Coppola, una sola parola a riguardo…”Orrore”

Ci sarebbe molto da commentare sull’argomento nucleare, ma vorrei dire giusto un paio di cose soffermandomi su due punti.

Primo: l’Europa progetta nuovi sistemi di sfruttamento delle fonti di energia rinnovabile: eolico, solare, geotermico, idrico, moto ondoso, manca poco che sfruttino persino l’energia dei terremoti per produrre corrente elettrica, mentre l’Italia cosa fa? Il Paese del Sole, che sorge su una delle aree geologicamente più attive, pensa a costruire nuove centrali nucleari, quando ancora deve finire di smantellare quelle costruite negli anni ’60.

Secondo: in Italia lo smaltimento dei rifiuti è nelle mani della camorra. Rifiuti tossici di ogni genere sono stati sotterrati sotto quelle che ora sono campagne di mele e pomodori. La maggior parte dei politici è corrotta e lo smaltimento delle scorie nucleari costa.
Quanto tempo credete dovrà passare, prima di poter trovare sul mercato la prima mela fosforescente?

Questo articolo rappresenta una sfida a tutti gli utenti che lo leggeranno.

Di seguito sono rappresentate alcune serie di numeri che si susseguono con una logica, provate a capire qual è, trovando i due numeri successivi di ognuna.
Le soluzioni sono cifrate in ROT13 per evitare click accidentali.

I nomi delle serie sono generati casualmente in Python.

Sfrinfralgubbro

Mostra soluzione ▼

Schiodo nistragobbe

Mostra soluzione ▼

Gliubbolgli trunmurpiri

Mostra soluzione ▼

Nacclastlonne

Mostra soluzione ▼

Linfonsgrisgu sfrittrariaco

Mostra soluzione ▼

Mussoqquedro (difficile!)

Mostra soluzione ▼

Drosophila melanogaster

Mostra soluzione ▼

L’uomo non sempre tende al progresso. A volte mette si ancora al presente per evitare il cambiamento. Ma ” l’unica costante del comportamento umano è il cambiamento ” ( Bruno Schettini ), quindi la scienza umana riesce, nonostante la morale, a fare dei significativi passi avanti. Le scoperte che vanno al di là dell’etica rientrano però, per forza di cose, nel elenco delle scoperte per serendipity: ovvero “cercare un ago in un pagliaio e trovarci la figlia del contadino” ( Julius Comroe Jr. ). Qualche esempio? L’America, la dinamite e… il viagra ( viagra e dinamite hanno più di una caratteristica in comune a quanto pare ). Ma anche nel caso specifico della psicologia ce ne sono di altrettanto clamorose: H.M. e i neuroni mirror.

H.M.

Per i pazienti affetti da crisi epilettiche c’era ben poco da fare nel 1953: o lobectomia ( asportazione delle aree in cui nascevano le crisi ) o sofferenza. Si scelse per la lobectomia: al paziente fu asportato il lobo temporale mediale bilaterale, area comprendente i 2 ippocampi, le 2 amigdale e parte delle corteccie paraippocampali. Zone di cui ai tempi poco si sapeva. L’operazione riuscì perfettamente, le crisi scomparvero e il Q.I. di H.M. salì da 104 a 118 ( per la scomparsa delle crisi ). Ma la perdita dei lobi asportati comportò la comparsa di una “fastidiosa” amnesia anterograda espilicita semantica, cioè: ” H.M. ora sono le 3 del pomeriggio”, passano 2/3 secondi e ” H.M. ora che ore sono?” “Boh!”. Grazie agli studi di Brenda Milner su questo paziente ora siamo in grado di conoscere le localizzazioni di gran parte delle memorie. Oggi esitono farmaci antiepilettici e il codice etico è contrario a terapie invasive…

Neuroni mirror

A cavallo tra gli anni  ’80 e 90′ Giacomo Rizzolatti e la sua equipe ( Uni. Parma ) stavano conducendo degli esperimenti su un gruppo di macachi, quando uno sperimentatore, mentre prendeva una banana,  notò casualmente l’attivazione di un area cerebrale del macaco che lo osservava. Il macaco era però rimasto fermo. Mai vista una cosa del genere. Si scoprì che nei macachi esiste una classe di neuroni che si attiva non quando il macaco compie un movimento, ma quando guarda qualcuno compiere un movimento. Nel ’95 lo stesso gruppo di lavoro ha scoperto un sistema analogo nell’uomo. Che vuol dire questa scoperta? Tutto e niente. Tutto perchè come suggerisce Ramachandran ” i neuroni specchio saranno per la psicologia quello che il dna è stato per la biologia “, niente perchè questa stessa teoria sembra essere smentita da lavori sperimentali che riducono l’importanza di questo sistema nell’uomo ( ” ci sono poche o nessuna evidenza a supportare l’ipotesi che il neurone mirror sottende l’azione e al contrario c’è una netta evidenza contro di esso” Greg Hickok ). Quanto tempo ci vorrà a scoprire la verità? Chiedetelo al codice etico.

Ecco un brano tratto dall’ultimo album di Ihsahn (After), On the shores, che combina l’arte del progressive metal con uno degli strumenti a fiato che più adoro, il sassofono.