Archivio tag per C++

Download Dev-C++ 4.0

16 Giu, 2009  5 Commenti

cpp1Nonostante la versione 4.0 di Dev-C++ sia abbondantemente superata (risale al 2000), risulta essere ancora molto utilizzata per merito dei suoi bassissimi requisiti minimi di sistema (Windows 95 e 32 MB di RAM).

Purtroppo è diventata quasi un’impresa riuscire a trovarla in giro, perché sul sito della software house (bloodshed) il link risulta danneggiato.

Per questo motivo ho deciso di pubblicarla qui, in modo che possa essere facilmente accessibile a tutti:

Download – Dev-C++ 4.0 – 21/09/2000

06-16-2009_11-55-39

Teorema di Laplace in C++

15 Giu, 2009  Commenti disattivi

laplaceIn questo articolo spiegherò come scrivere un programma in C++ che calcoli il determinante di una matrice utilizzando il Teorema di Laplace.

Il Teorema di Laplace afferma: “Data una matrice quadrata di ordine n, il suo determinante è uguale alla somma dei prodotti degli elementi di una qualsiasi riga (o colonna) per i rispettivi complementi algebrici“.
Il complemento algebrico dell’elemento aij appartenente alla matrice M, è il determinante della matrice che si ottiene cancellando la i-esima riga e la j-esima colonna dalla matrice M, preso con il segno + se i+j è pari, segno – se i+j è dispari.

M = \left( \begin{matrix} a_{11}&\underline{a_{12}}&a_{13}\\ a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33} \end{matrix} \right)
A_{12} = (-1)^{1+2}\cdot\left| \begin{matrix} a_{21}&a_{23}\\ a_{31}&a_{33} \end{matrix} \right|
\left|\text{M}\right|=a_{11} \cdot A_{11}-a_{12}\cdot A_{12}+a_{13} \cdot A_{13}

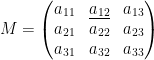
Leggi il resto dell’articolo »