Archivio tag per Teoremi

Un rudimentale tubo di Pitot

15 Mar, 2010  5 Commenti

Durante gli studi di ingegneria aerospaziale, ho incontrato questo simpatico strumento che è il tubo di Pitot.
La sua funzione, che è ampiamente descritta su Wikipedia, è quella di misurare la velocità di un fluido.

Il tubo di Pitot è costituito da un tubo, di una generica lunghezza, disposto parallelamente alla direzione del fluido (in particolare, al vettore velocità). Un’estremità del tubo è aperta, per permettere l’ingresso del fluido, mentre l’altra estremità è collegata ad un manometro. I manometri che si possono utilizzare sono i più disparati, quello che ho utilizzato io sfrutta la Legge di Stevino.

p_{sta}=-\rho g \Delta z\\\\p_{sta}:\text{Pressione statica}\\\rho :\text{Densita

Com’è possibile vedere nell’immagine qui sopra, il manometro e il tubo di Pitot non sono altro che un semplice tubo pieno d’acqua, collegati ad una scala millimetrata che permette di misurare il dislivello della colonna d’acqua. In condizioni iniziali, il livello dell’acqua segnato è 13.8 mm.
(Attenzione: la scala millimetrata posta accanto al manometro serve per misurare le variazioni di quota dell’acqua, non l’altezza assoluta. È questo infatti il dato necessario per calcolare la pressione.)

Ho colorato l’acqua con dell’inchiostro nero, in modo da poter visualizzarne meglio il dislivello all’interno nel tubo. L’inchiostro non ha la stessa densità dell’acqua, ma data la natura qualitativa di questo esperimento, la variazione di densità dovuta alla sua presenza è del tutto trascurabile.

Il tubo di Pitot si trova in genere sugli aerei e misura la velocità dell’aereo rispetto all’aria. Data la difficoltà nel testare il tubo di Pitot in condizioni di moto rispetto al fluido, il modo più semplice per verificarne il funzionamento è quello di mettere in moto l’aria rispetto allo strumento, tenendo quindi fermo il tubo. Ciò che conta è infatti il moto relativo tra il fluido e il corpo.

L’oggetto che ho utilizzato per mettere in moto l’aria è un semplice phon.
Indirizzando infatti il getto del phon parallelamente al tubo, è possibile misurare la velocità dell’aria che esce da questo.

Come è possibile vedere dalle immagini, la colonna d’acqua nel tubo subisce una variazione di quota di circa 1.9 cm.
Per la Legge di Stevino, la pressione legata a questa variazione di quota è:
p_{sta}=-\rho g \Delta z=-(1000 kg/m^3)(-9.81 m/s^2)(0.019 m)=186 Pa

L’aria che entra all’interno del tubo, alla velocità incognita V, genera una pressione dinamica che è:
p_\text{din}=\frac12\rho V^2\\p_\text{din}:\text{Pressione dinamica}\\\rho:\text{Densita

Questa pressione va a bilanciare la pressione statica che abbiamo trovato con la Legge di Stevino, quindi:
p_\text{sta}=p_\text{din}=186 Pa

Dall’espressione della pressione dinamica, ormai nota, è possibile ricavare la velocità del fluido:
V=\sqrt{\frac{2p}\rho}=\sqrt{\frac{2\cdot 186 Pa}{1.225 kg/m^3}}=17.4 m/s

La velocità dell’aria che esce dal mio phon è di circa 17.4 m/s (o anche 62.6 km/h). Come valore della densità dell’aria ho utilizzato quello della tabella disponbile su Wikipedia, alla gelida temperatura del mio garage di 15°C.

È importante notare che la densità utilizzata nella Legge di Stevino è la densità dell’acqua, mentre la densità utilizzata nell’espressione della pressione dinamica è la densità dell’aria.

Volendo approfondire un po’ l’argomento, bisogna tenere presente il fatto che il tubo di Pitot non misura soltanto la pressione dinamica, ma misura la pressione totale, che per il Teorema di Bernoulli è:
p_\text{tot}=p_\text{stat}+p_\text{din}=p_\text{stat}+\frac12\rho V^2

Per conoscere quindi la pressione dinamica, occorrerebbe conoscere anche la pressione statica attorno al tubo, che viene misurata utilizzando una seconda presa d’aria sul collo del tubo e va sottratta alla pressione totale. Però, nelle condizioni in cui ho effettuato l’esperimento, il manometro utilizzato è soggetto alla stessa pressione statica a cui è soggetto il tubo di Pitot, che è la pressione atmosferica. Quindi il valore misurato tramite il dislivello della colonna d’acqua è già la pressione dinamica.

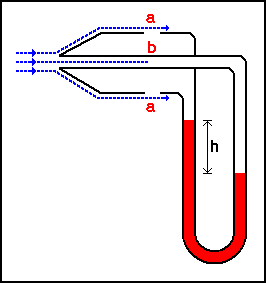
Com’è infatti possibile vedere da questa immagine, la pressione totale misurata tramite la presa d’aria b, viene confrontata con la pressione statica misurata dalle due prese d’aria a. Il dislivello h misurerà precisamente la pressione dinamica.

Teorema di Laplace in C++

15 Giu, 2009  Commenti disattivi

laplaceIn questo articolo spiegherò come scrivere un programma in C++ che calcoli il determinante di una matrice utilizzando il Teorema di Laplace.

Il Teorema di Laplace afferma: “Data una matrice quadrata di ordine n, il suo determinante è uguale alla somma dei prodotti degli elementi di una qualsiasi riga (o colonna) per i rispettivi complementi algebrici“.
Il complemento algebrico dell’elemento aij appartenente alla matrice M, è il determinante della matrice che si ottiene cancellando la i-esima riga e la j-esima colonna dalla matrice M, preso con il segno + se i+j è pari, segno – se i+j è dispari.

M = \left( \begin{matrix} a_{11}&\underline{a_{12}}&a_{13}\\ a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33} \end{matrix} \right)
A_{12} = (-1)^{1+2}\cdot\left| \begin{matrix} a_{21}&a_{23}\\ a_{31}&a_{33} \end{matrix} \right|
\left|\text{M}\right|=a_{11} \cdot A_{11}-a_{12}\cdot A_{12}+a_{13} \cdot A_{13}

Leggi il resto dell’articolo »

Io VORREI studiare, ma…

11 Mar, 2009  2 Commenti

studiareDevo studiare. Vorrei anche farlo, ma il problema è che ogni volta rimando di un certo tempo.
Parto ponendomi di studiare tra 2 minuti, dopo 2 minuti rimando di un altro minuto, poi di mezzo, poi di un terzo e così via…

A prima vista, si potrebbe pensare che prima o poi il tempo dovrà essere così breve da costringermi ad iniziare a studiare, ma purtroppo non è così! Infatti il tempo che impiegherò per mettermi a studiare è:
\text{Tempo: }2+1+\frac12+\frac13+\dots+\frac1n\text{ minuti}

Questo tempo, è sicuramente più grande del numero:
2+1+\frac12+\frac14+\frac14+\frac18+\frac18+\frac18+\frac18+\frac{1}{16}+\dots+\frac{1}{16}+\dots

Questo numero può essere scritto come:
2+1+\frac12+\text{(4-2) volte}\frac14+\text{(8-4) volte}\frac18+\text{(16-8) volte}\frac{1}{16} …e così via

Cioè:
2+1+\frac12+\frac12+\frac12+\frac12+\frac12+\frac12+\frac12+\frac12\dots, che è un numero infinito.

Dato che il tempo dopo il quale inizierò a studiare è più grande del numero qui sopra scritto, deve essere più grande di infinito!
Per questo motivo, inizierò a studiare tra «infiniti minuti».

Per quanto possa sembrare stupido questo discorso, esso rappresenta la dimostrazione della cosiddetta serie armonica, che è divergente e in matematica viene rappresentata come:
\sum_{n=1}^{\infty} \frac{1}{n}

Detto questo, se dovete iniziare a studiare, fatelo adesso o non inizierete mai più 😀